Dopo aver parlato di equiestensione e isoperimetria, aver manipolato poligoni con stessa area e diverso perimetro, con stesso perimetro di diversa area o con uguale area e perimetro, ho proposto ai bambini, grazie alla scheda di @emozioniinmatematica , il problema di Didone, la principessa che riuscì a fondare una nuova città grandissima partendo da una pelle di bue.

Ho chiesto ai bambini come avrà fatto a risolvere il problema Didone e dopo un’accesa discussione, e ipotesi strampalate, ho dato un suggerimento: ho detto di fissare l’attenzione sulla parola “contenere” e di pensare al riferimento della parola “contenere” rispetto ai poligoni.

Piano piano le ipotesi state un po’ più pratiche e siamo arrivati alla risoluzione del problema. Bisogna fare striscioline sottili per ottenere una corda la più lunga possibile che possa contenere al suo interno un territorio il più ampio possibile.
Proviamoci dunque anche noi. Ho proposto ai bambini un pezzo di stoffa di cotone e ho chiesto di stimare la lunghezza della corda che ne avremmo potuto ricavare.
Abbiamo poi cominciato, divisi in gruppi, a tagliare striscioline e annodarle fino ad ottenere delle matasse di corda di cotone.






Le abbiamo poi annodate tutte tra loro e cominciato a misurarle, ma subito ci siamo resi conto che lo spazio a nostra disposizione, corridoio o cortile della scuola, non erano sufficientemente ampi.



Ci siamo dunque spostati nel vicino campo sportivo e lì abbiamo srotolato le nostre matasse, e con un metro a nastro abbiamo misurato la lunghezza della corda.



È stato incredibile ed entusiasmante….
Nessuno di noi si sarebbe mai immaginato che questa nostra corda misurasse circa 95 metri, calcolando anche che per annodarla spesso se ne è sprecata un po’.

Questa Didone era davvero una ganza!
Era una ragazza intelligente che ha messo a frutto le sue doti logiche.
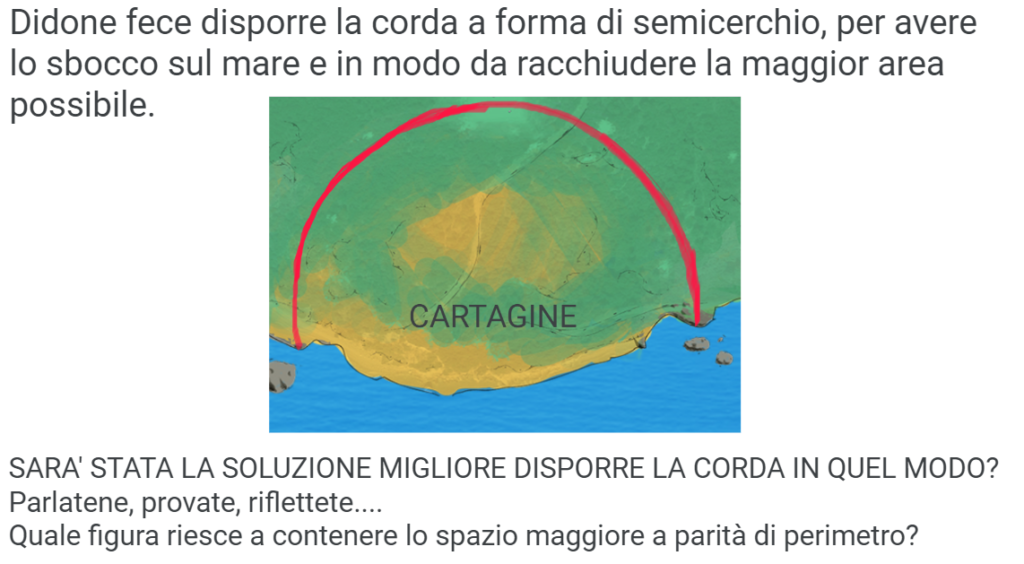
A questo punto la domanda che ci è venuta è stata: Didone ha disposto la sua corda lunghissima a semicerchio perché voleva conservare lo sbocco sul mare, ma la sua scelta sarà stata la migliore? È il cerchio la forma che ha più area a parità di perimetro?
…continueremo a lavorare e ad indagare…appuntamento alla prossima puntata!!! 😉

Il dire e il fare. Il fare lascia sicuramente il segno, specialmente nei bambini.
Dovrebbe essere la base dell’insegnamento.